
Theory For FOC Control-2
前言
在上章節介紹完馬達種類與簡單描述控制方法,這章節會進入數學模型與FOC控制方法深入介紹
控制狀態

這邊可以參考左圖轉動動態圖,可以看到不同的電流方向通過
讓定子產生磁場方向,轉子因異極相斥進而產生旋轉。
而這種旋轉狀態可以再細分為6種狀態,下面分別對各種狀態探討

上圖六種不同的電流方向把其表格化就可以獲的下圖,其中六個步驟正處於哪一步驟就取決於轉子位置,轉子位置通常可由Sensor感知或由無通電那一極感知返電動式去推算現在轉子位置

再由上圖把其電流圖表化就可以獲得下圖,而怎實現下圖就出現三相逆變電路(這邊就會對應BLDC的motor driver)

PS:這邊注意上圖看起來很像六步方波驅動BLDC但細看會發現這邊是電流六步方波是電壓
三相逆變電路

上面電路的 VT 是指 IGBT 模塊,而在小功率驅動中一般使用 MOSFET 来當做開關,兩者皆為全控器件,用途可以等同MOS管,可以看作電壓控制的高速電子開關,在MOS管的極閘(上图中的High Drive和Low Drive)施加高電頻或者低電頻,就可以控制MOS原極和漏極的導通或者關閉。
在下圖中,我們打打第一组半橋的上橋臂、第二组和第三组半橋的下橋臂(其餘的關閉),即打開 V T 1 , V T 2 , V T 6 VT1,VT2,VT6VT1,VT2,VT6 ,那麼就可以讓電流從電源正極流過馬達的a相,流經b、c相,然後回到電源負極:

下圖為上面兩臂,下面一臂的情况:

通過控制三个半橋的不同開關狀態,我們可以控制電流在馬達中的不同流向了。
這樣,在任一瞬間,將有三个橋臂同時導通。可能是上面一個臂下面兩個臂,也有可能是上面兩個臂下面一個臂。因为每次換向都是在同一相上下兩個橋臂之間進行,因此也被稱為縱向換流。
Clarke’s Transformation與 Park’s Transformation
這邊先有一個概念,電流輸出要直接控制成弦波,對於元件要求與控制手段都是非常嚴苛的,因此有沒有甚麼方式可以把弦波轉呈線性呢?所以就演變出 Clarke與 Park 轉換,給各位看2張圖就會比較明這2個轉換是在幹嘛了˙
Clarke’s Transformation
其中Clarke’s Transformation是先把3個弦波簡化成2個旋波(這邊簡化方法簡單說是座標轉換)

Park’s Transformation
Park’s Transformation再來把2個弦波轉變成2線性直線

數學公式
首先我們看馬達在轉動時後的慣性坐標系


如上圖可以看到三個不同輸入電壓弦波所產生的合力方向,首先觀察通入電流在這座標系變化,來做回授訊號控制,第一步Clarke’s Transformation把慣性坐標系轉到正交座標αβ 座標系

如上圖把2座標系重合,其中N3為abc座標三相繞組每相的有效匝數,N2為αβ 座標系繞組每相的有效匝數
這邊注意這個座標轉換要滿足下面2點
- 變換前後電流所產生旋轉磁場要等效
- 變換前後馬達功率不變


由上公式等效投影到αβ 座標系並把它寫成矩陣形式如右上,但上面公式不能逆轉換因此需在改變,多一個0軸(這邊0軸大多時候並不重要可以忽略)


由右邊推導最後可以求得如下
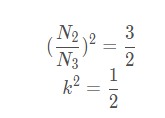
然後等幅變換過程如下


因为要求等幅值,Ib與Ia相位相同且α比β相位超前90度,可以簡化成下公式


總結
Clarke轉換公式如下



看完Clarke’s Transformation接下來就是要把弦波轉呈線性的Park’s Transformation


這邊Park’s Transformation就只是比較簡單的慣性座標轉成非慣性座標系(假想坐標系)來去看就可以簡化成線性關西

總結

